Как мы учим умные фабрики быть отзывчивыми с помощью протокола робономики

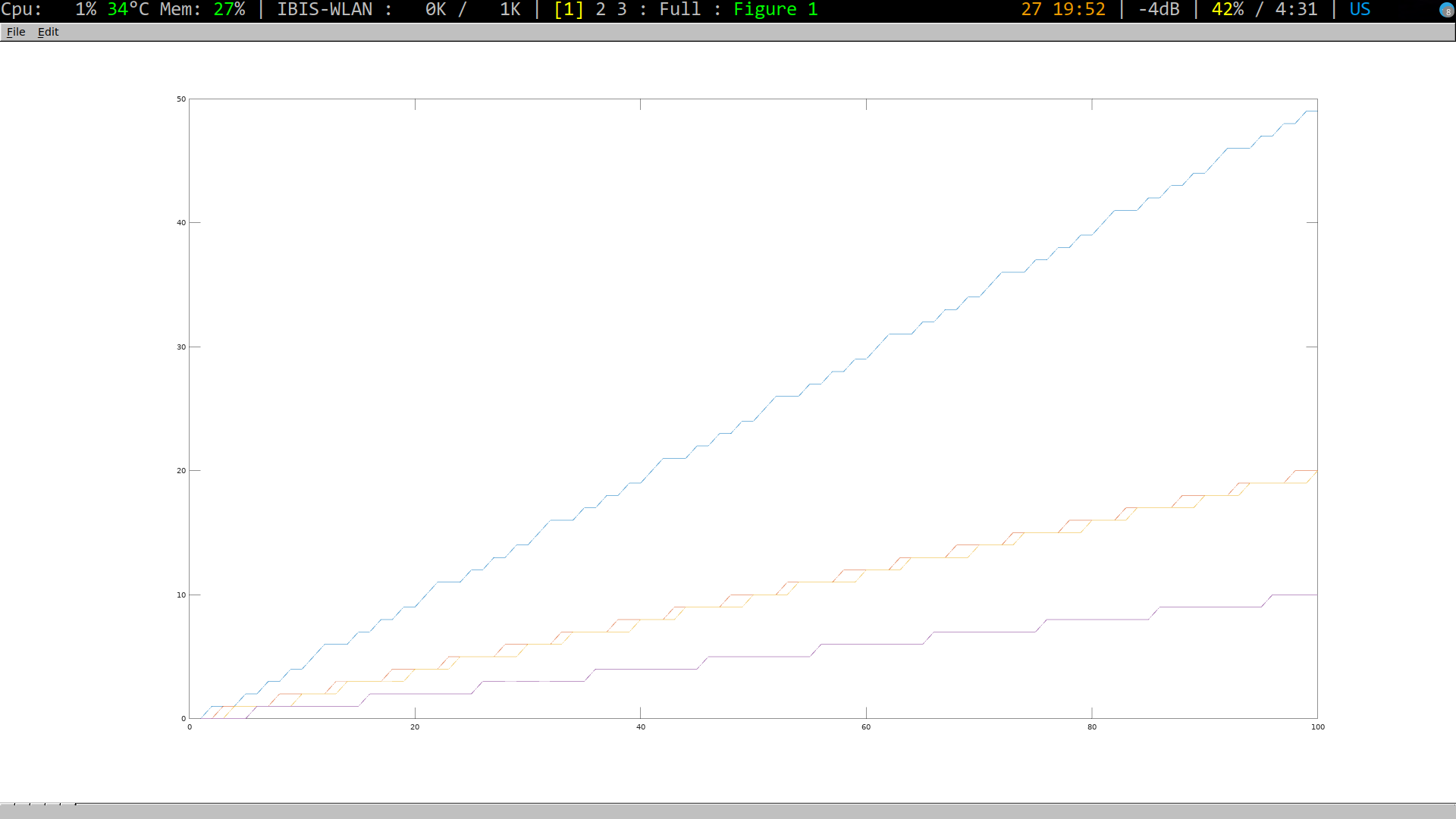
На финишную прямую вышли работы по сборке демонстрационного стенда Индустрия 4.0, и в скором времени модель, состоящая из двух логистически-складских служб и четырех умных фабрик, работающих под управлением промышленных контроллеров Siemens, прибудет к нам на Волгу.

Данный демонстрационный стенд позволит начать множество экспериментов по созданию моделей поведения киберфизических систем, говорящих между собой и с человеком на одном языке – языке экономики.

Первая важная часть стенда Индустрия 4.0 – это демонстрация отзывчивости умных фабрик к изменениям капитала на рынке с помощью протокола робономики. Своей работой мы отвечаем на вопросы, почему роботы должны отзываться на изменение капитала на рынках и как это возможно реализовать.

Почему умные фабрики должны отзываться на изменения капитала на рынках

Инвестор, находясь в процессе распределения своего капитала, с одной стороны, стремится компенсировать недостаток предложения на рынке,  и, с другой стороны, извлекает свой капитал на тех рынках, где переизбыток капитала приводит к перенасыщению предложением.

Помимо недостатка и перенасыщения капиталом рынков, также, важным критерием является размер трансакционных издержек, которые готов нести потребитель. Чем выше издержки, тем инвестору интереснее будет рынок, так как часть издержек можно превратить в выручку компании.

Смотря с другой стороны на данное поведение, можно сказать, что предложение на рынке изменяется вследствие перераспределения инвесторами капитала. Тем самым производители стремятся уменьшить ошибку распределения своих производств по рынкам вслед за капиталом и уменьшают рассогласование системы производства-потребления в целом.

Инвесторы получаются никем иным, как оракулами внешнего мира для экономики.

Получается следующее правило игры: при правильном понимании текущего и потенциального состояния системы инвестор поощряется доходом на размещенный капитал и наказывается уменьшением капитала за неправильный прогноз потребительского спроса. Данный стимул приводит к рациональному поведению инвесторов, как ответственных в обществе за распределение предложения, и тем самым может использоваться как маяк для полностью автоматизированных предприятий по выбору рынков своей работы.

Как умные фабрики будут отзываться на изменение капитала

Представим множество экономически самостоятельных киберфизических систем или просто роботов как вектор (R), а капитал (инвестиции) — как вектор (K). Здесь вектор R = {R_i, i=\overline{1,n}}, где R_i — количество роботов на рынке i, n — количество рассматриваемых рынков. А вектор K = {K_j, j=\overline{1,n}}, где  K_j — инвестиции в j-й рынок. Сформулируем описание модели пропорционального капиталу распределения роботов на рынке следующим образом:

R'[k] = K[k] * { \sum R_i[k] \over \sum K_i[k] }

e[k] = R'[k] - R[k-1] ;

Здесь:

  • R'[k] — желаемое распределение роботов на рынках [штук];
  • R[k-1] — количество роботов, уже присутствующих на данном рынке капитала;
  • e — вектор ошибок распределения (отклонение от желаемого значения распределения) [штук];
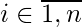  • i \in \overline{1,n} — индекс рынка;
  • k — шаг дискретного времени;
  • \sum R_i[k] — количество роботов на всех рассматриваемых рынках на шаге k;
  • \sum K_i[k] — объём инвестиций в рассматриваемые рынки на шаге k.

Исходя из выше описанного, можно сформулировать закон управления экономикой роботов следующим образом:

Каждый робот должен стремиться к участию на том рынке, где ошибка распределения выше.

При включении очередного робота в экономику рынок для размещения своего предложения этим роботом выбирается из равенства:

i = maxi(e[k]), что приводит к e_i[k] \rightarrow 0

Здесь maxi(e) — индекс максимального элемента вектора отклонения.

Алгоритм выборки: анализ капитала и предложений

Рассмотрим пример такого распределения роботов при условии, что у нас есть следующие распределение капитала K = {Рынок А: 500, Рынок Б: 200, Рынок В: 200, Рынок Г: 100} и шесть роботов, которые должны быть распределены на эти 4 рынка.

Начальное положение:

=====================

Рынок | Объем капитала | Роботов

—————————

Рынок А | 500 | 0

Рынок Б | 200 | 0

Рынок В | 200 | 0

Рынок Г | 100 | 0

Появление первого робота в системе демонстрирует следующие показатели отклонения: {0.50000, 0.20000, 0.20000, 0.10000}. Робот выбирает рынок с наибольшим отклонением, т.е. первый.

Рынок А | 500 | 1

Рынок Б | 200 | 0

Рынок В | 200 | 0

Рынок Г | 100 | 0

Как получились показатели отклонения: {0.50000, 0.20000, 0.20000, 0.10000}.  Для начала считаем желаемое количество роботов на рынке (R’):

R'(Рынок А) = Капитал на Рынке А * (Сумма всех роботов/Сумма всего капитала) = 500 * 1/1000 = 0.5

R'(Рынок Б)  = 200 * 1/1000 = 0.2

R'(Рынок В)  = 200 * 1/1000 = 0.2

R'(Рынок Г)  = 100 * 1/1000 = 0.1

Теперь посчитаем отклонение (e):

e(Рынок А) = Желаемое количество роботов — реальное количество, присутсвующих уже на рынке роботов = 0,5 — 0 = 0,5

e(Рынок Б) = 0,2 — 0 = 0,2

e(Рынок В) = 0,2 — 0 = 0,2

e(Рынок Г) = 0,1 — 0 = 0,1

Появление второго робота в системе демонстрирует следующие показатели отклонения: {0.00000, 0.40000, 0.40000, 0.20000}. Робот выбирает рынок с наибольшим отклонением, т.е. второй или третий.

Рынок А | 500 | 1

Рынок Б | 200 | 1

Рынок В | 200 | 0

Рынок Г | 100 | 0

Как получились показатели отклонения: {0.00000, 0.40000, 0.40000, 0.20000}.  Для начала считаем желаемое количество роботов на рынке (R’):

R'(Рынок А) =  = 500 * 2/1000 = 1.0

R'(Рынок Б)  = 200 * 2/1000 = 0.4

R'(Рынок В)  = 200 * 2/1000 = 0.4

R'(Рынок Г)  = 100 * 2/1000 = 0.2

Теперь посчитаем отклонение (e):

e(Рынок А) = Желаемое количество роботов — реальное количество, присутсвующих уже на рынке роботов = 1 — 1 = 0

e(Рынок Б) = 0,4 — 0 = 0,4

e(Рынок В) = 0,4 — 0 = 0,4

e(Рынок Г) = 0,2 — 0 = 0,2

Появление третьего робота в системе демонстрирует следующие показатели отклонения: {0.50000, -0.40000, 0.60000, 0.30000}. Робот выбирает рынок с наибольшим отклонением, т.е. третий.

Рынок А | 500 | 1

Рынок Б | 200 | 1

Рынок В | 200 | 1

Рынок Г | 100 | 0

Как получились показатели отклонения: {0.50000, -0.40000, 0.60000, 0.30000}.  Для начала считаем желаемое количество роботов на рынке (R’):

R'(Рынок А) =  = 500 * 3/1000 = 1.5

R'(Рынок Б)  = 200 * 3/1000 = 0.6

R'(Рынок В)  = 200 * 3/1000 = 0.6

R'(Рынок Г)  = 100 * (3/1000) = 0.3

Теперь посчитаем отклонение (e):

e(Рынок А) = 1,5 — 1 = 0

e(Рынок Б) = 0,6 — 1 = (- 0,4)

e(Рынок В) = 0,6 — 0 = 0,6

e(Рынок Г) = 0,3 — 0 = 0,3

Появление четвертого робота в системе демонстрирует следующие показатели отклонения: {1.00000, -0.20000, -0.20000, 0.40000}. Робот выбирает рынок с наибольшим отклонением, т.е. первый.

Рынок А | 500 | 2

Рынок Б | 200 | 1

Рынок В | 200 | 1

Рынок Г | 100 | 0

Появление пятого робота в системе демонстрирует следующие показатели отклонения: {0.50000, 0.00000, 0.00000, 0.50000}. Робот выбирает рынок с наибольшим отклонением, т.е. или первый или четвертый.

Рынок А | 500 | 3

Рынок Б | 200 | 1

Рынок В | 200 | 1

Рынок Г | 100 | 0

Появление шестого робота в системе демонстрирует следующие показатели отклонения: {0.00000, 0.20000, 0.20000, 0.60000}. Робот выбирает рынок с наибольшим отклонением, т.е.  четвертый.

Рынок А | 500 | 3

Рынок Б | 200 | 1

Рынок В | 200 | 1

Рынок Г | 100 | 1

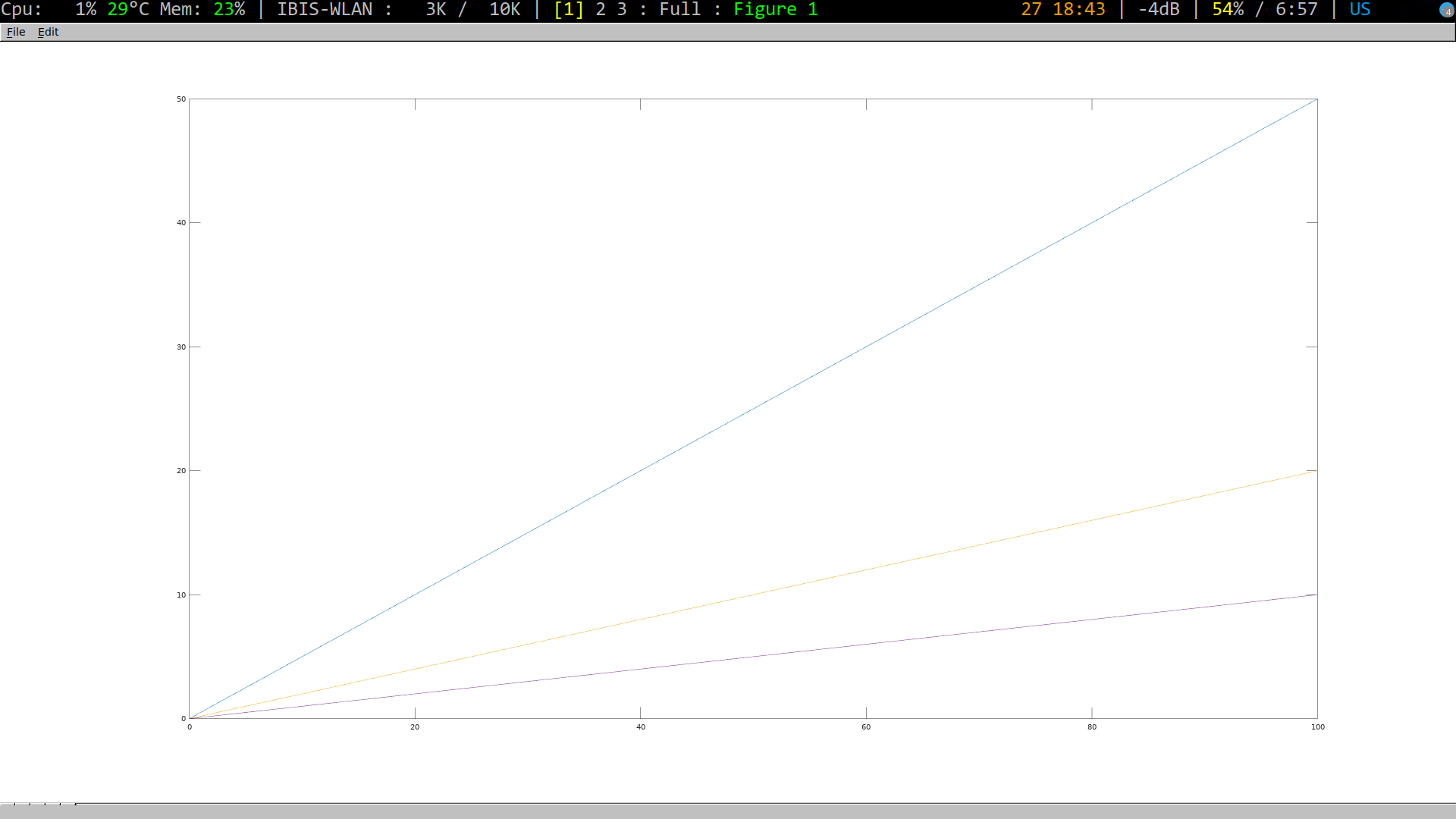
Дополняем пример графиком роста до 100 роботов всего:

Рис. 1 по оси X отражаем рост общего количества роботов в системе. По оси Y желаемое распределение по рынкам.
Рис. 1 по оси X отражаем рост общего количества роботов в системе. По оси Y — желаемое распределение по рынкам.
Рис. 1 по оси X отражаем рост общего количества роботов в системе. По оси Y желаемое распределение по рынкам.
Рис. 2 по оси X отражаем рост общего количества роботов в системе. По оси Y — реальное распределение по рынкам.

В заключение

Это первая модель поведения киберфизических систем, как экономических агентов, которую мы заложим в протоколе робономики и продемонстрируем в физической модели. Архитектура дистрибутива AIRA разрабатывается нами таким образом, чтобы данный модуль мог быть заменен в реальном времени работы каждого отдельного агента.

Как мы учим умные фабрики быть отзывчивыми с помощью протокола робономики: 2 комментария

  1. Интересная статья.
    Только мне кажется, что термин «ошибка распределения» должен быть заменен на что-то вроде «разница» или «отклонение». Потому что вот эта фраза на первый взгляд кажется нелогичной:

    «Каждый робот должен стремится к участию на том рынке, где ошибка распределения выше». Потом читаешь и понимаешь логику (она обратная мне привычной)) Может быть, конечно, это больше философский вопрос, но в prediction market’ах «ошибка» предсказания именно ошибка и ничто другое.

    Ну собственно, не до конца мне понятно, чем же «роботы» отличаются от «не роботов».
    Если я вот сейчас сделаю DAO с акторами, который будут работать с Aira, но без актуаторов и «рук», «умных замков», «чего-то иного физического» — то это будет же уже не робот, а значит это не ваша ЦА? Зачем такое искусственное разграничение? Чем вам RasperryPI без клешни не устроит, который что-то делает имея экономические мотиваторы и управление?

    p.s. Спасибо за блог, читаю.

    Ответить

    1. Искусственного разграничения нет. Дело в том, что нами выбрана для работы на 2017 — 2018 год область IoT и Индустрии 4.0, и так как мы общаемся сейчас в основном с людьми в этой области, то и документация получается с приведением примеров на киберфизических системах такого типа — сенсоры, умные заводы, автопилотируемые ТС. Если у тебя есть сервисы, как автономные экономические агенты и ты используешь AIRA, то супер! Расскажи подробнее, как будет результат, а мы поможем. Не забывай пользоваться помощью наших devops, если что будет не понятно.

      Ответить

Добавить комментарий

Ваш e-mail не будет опубликован. Обязательные поля помечены *